MDF and Alpha (frequency of defense and attack) in poker - what are these indicators and how are they calculated

Translated with the help of AI. We apologize for any errors and would appreciate your help in correcting them.

Translated by order of the educational portal university.poker
Author: Tombos21, Original Source: GTO Wizard

1. Minimum Protection Frequency (MDF) and Aggression Frequency (?) in Poker

Minimum Protection Frequency (MDF) and Aggression Factor (?) are key mathematical indicators in poker that help players make optimal decisions when defending against bet and choosing the frequency of bluff. They determine how often to protect your hand and how likely it is to bluff in order to remain unexploited.

If you defend too broadly, your villain can beat you with vellum bets. If you defend too secretly, he can confuse you with a bluff. Thus, with a good strategy, we will need to call just enough to make the bluff of the opponent indifferent to equity. This indicator has certain limitations in practical application, but remains a fundamental element of theoretical poker.

2. What is the minimum protection frequency (MDF)

The minimum protection frequency is an indicator that shows how often you need to call so that your opponent's hands with zero equity are indifferent to bluff or fold. The MDF score in poker simply ensures that your opponent will not be able to bluff profitably with any two cards. You need to observe the minimum frequency so as not to get hit by a bluff.

MDF is a risk/reward calculation designed to make your opponent's bluff equal to 0 EV. 

3. What is considered “protection”

To defend means to continue. You can defend yourself with a raise or a call. Both options will be considered protection.

4. Important Warning

MDF should be seen as a shield to stop your opponent from excessive bluff. First of all, you need to understand this right away.

Do not use MDF if your opponent is not bluff enough.

There is no point in trying to make his bluff EV zero if he is clearly not bluffing enough bluff. Lower your shield and start using overfolds against opponents who often bet a lot only on the vellya value. MDF should only be used as a shield to prevent you from being confused by the bluff.

5. What is Alpha

If Minimum protection frequency (MDF) is your shield, Alpha is your sword! Alpha is the inverse.

The alpha (?) is an inverse value showing how often the opponent should fold against your bluff with zero equity so that you at least do not lose money on such a game.

Alpha is a formula that reflects the risk/reward ratio, allowing you to calculate how often an opponent should defend so that your bluff remains breakeven. If the opponent folds more often than the theory requires, this is a great opportunity for profitable bluff. However, if it is defended too broadly, it may be worth reconsidering the frequency and situation for the bluff.

1. ? = 1 – MDF
2. MDF= 1 –?

6. Calculation

Formula

In this risk/reward calculation, the bet relative to the pot is taken into account in order to calculate the total frequency of protection necessary for bluff to be indifferent. The formula for calculating MDF/α is very simple.

Alpha (α) = Risk / (Risk + Reward), where:

1. Risk is the amount of bet you put into a bluff as a bluff.
2. The reward is the pot that you will win if the villain defolds.

Another formula you can use concerns the size of bet and pots. I don't like this formula because it doesn't work with the raise but only works for the initial bet. But I'll still leave it here for your information. 

1. MDF = pot / (pot + bet)
2. bet / (pot + bet)

Example 1

You put $60 into a $100 pot. Find Alpha and MDF :

In order for your bluff not to lead to losses, the villain must cheat at least in 37.5% of cases.

1. MDF is just 1 – α
2. MDF = 1 – 37.5% in this case, which is 62.5%. 

Therefore, the opponent should defend a minimum of 62.5% of their range so that your bluff remains breakeven. If its protection turns out to be less frequent, bluff will become profitable, and with more frequent protection, it will begin to lead to losses.

Example 2

You bet $60 in a $100 pot and your villain makes a raise of up to $200. What is your MDF and Alpha? Your villain risked $200 to win the pot ($100 + $60).

Therefore, to prevent a profitable bluff-raise from the opponent with any two cards, it is necessary to protect 44.5% of your bet range against such an increase. Conversely, it needs you to dump at least 55.5% of your bet range to have a profitable net bluff.

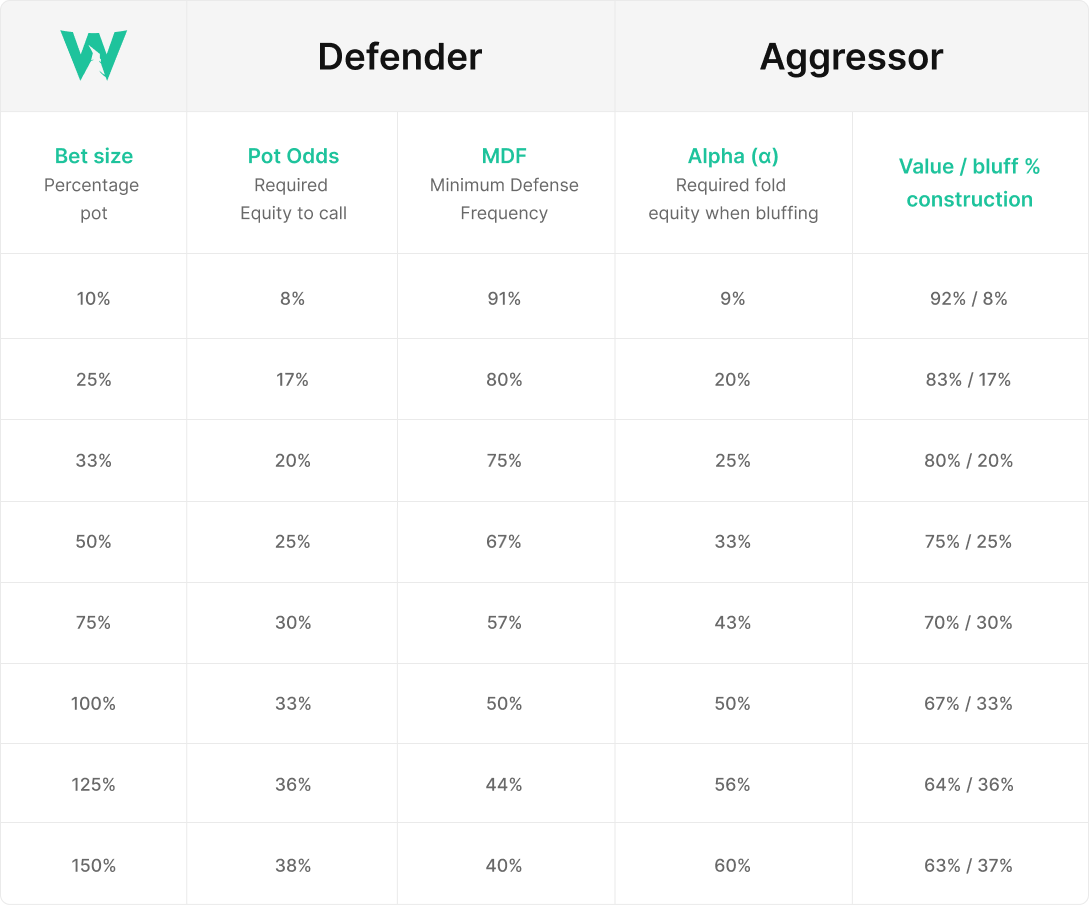
Cheat sheet

Some players simply use the cheat sheet to evaluate Alpha and MDF depending on the size of the bet. For your convenience, we made a cheat sheet like this. To use it, simply look at the bet size in the first column and find the appropriate Alpha/MDF value in the third and fourth columns.

Important note: these numbers are only valid for the initial bet! MDF and Alpha change during the raise and cannot be determined only by the bet size as a percentage of the bank pot.

7. Calculations of expected value (EV)

MDF and Alpha define only the break-even point. However, using a simple formula for the expected value, we can calculate the real profitability of a pure bluff. It also allows us to analyze the profitability range depending on the width of the opponent's call.

The expected value of a pure bluff is expressed as follows:

EV (bluff) = (% fold × jar size) – (% call × bet value).
This works because the pot is the amount we get when the opponent villain folds, and our bet is how much we lose when he calls. In the meantime, we will assume that our bluff always loses when we are called.

Example 3

We perform overbet in the amount of 125% of the pot with a clean bluff on the river. Villain accepts a call in 40% of cases. In this calculation, we assume that the size of the bank is $100 pot.

The formula of the expected value for a pure bluff:

1. EV (bluff) = (% fold × pot) – (% call × bet)
2. EV (bluff) = (60% × 100$) – (40% × 125$) = 10$.

So the EV of this bluff is $10 because our villain is overfolded! So how often does an opponent need to fold for our bluff to cost $0?

1. Alpha = Risk / (Risk + Reward) = 125 / (125 + 100) = 55.5%

In other words, if it defends 44.5% of its range, this overbet bluff will break even. But as it refills slightly, it becomes profitable!

Schedule

Let's depict the profitability of our bluff as a percentage of the fold:

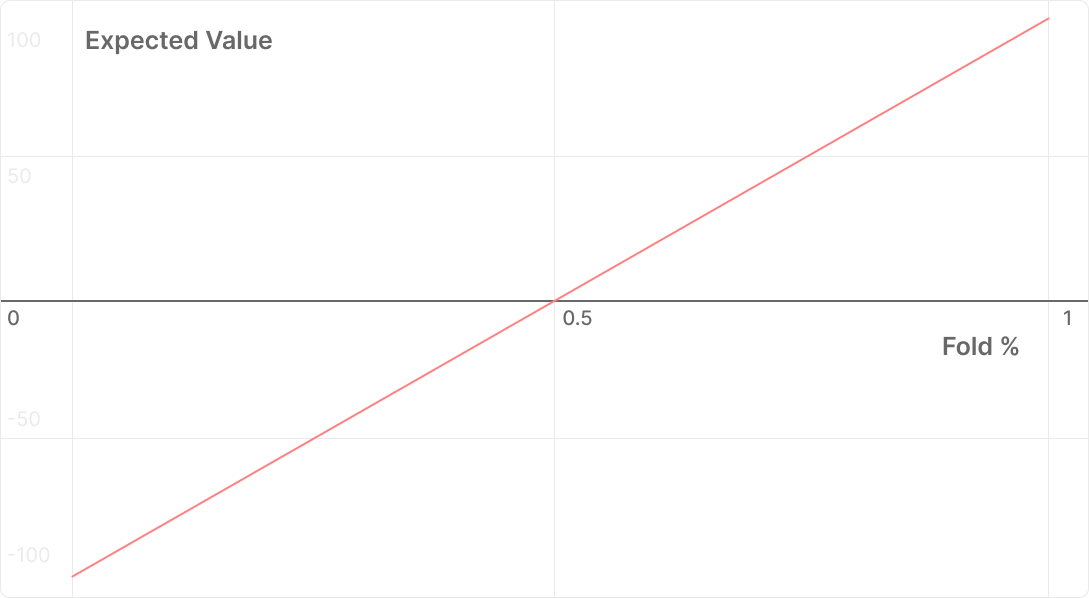
• The less often an opponent discards cards (the left part of the chart), the more losses our bluff (downward movement) brings, up to the maximum amount put at risk.
  On the contrary, the more often he discards cards (the right side of the chart), the higher the profitability of our bluff (upward movement), reaching the limit in the size of the entire pot.

• From the point of view of geometry, it is possible to draw a straight line from the point (0, -125) to (1, 100). The intersection point of this line with the X-axis shows the minimum percentage of folds required to break even of the bluff. In this case, this value exactly corresponds to Alpha — 55.5%.

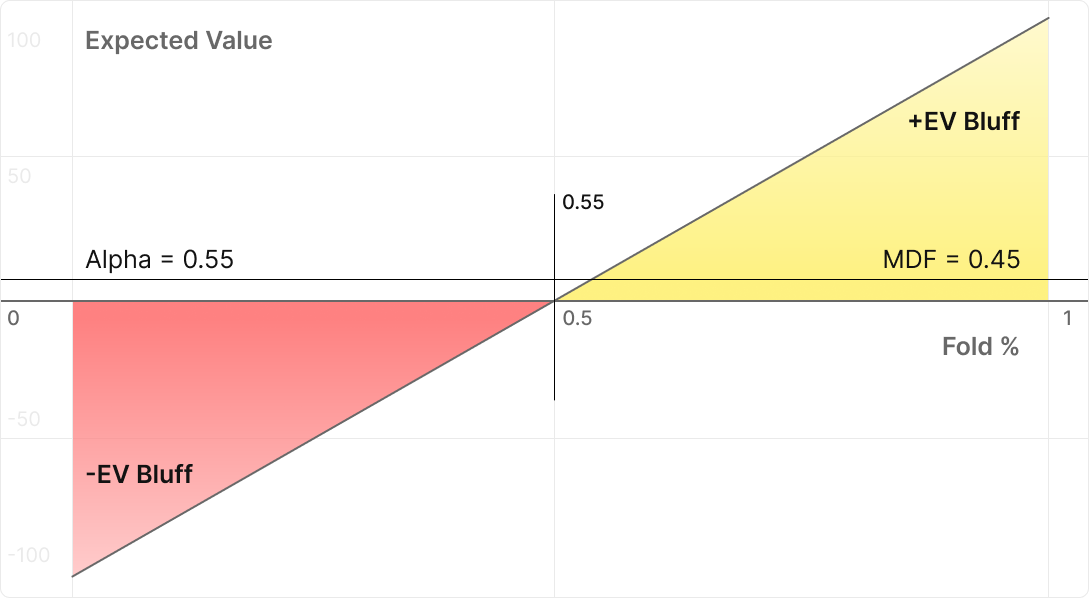
Let's visualize this graph with color highlighting.

1. On the right is the +EV zone, where the villain discards cards more often than 55% of the time, making our bluff profitable.
2. On the left is the -EV zone, where its fold frequency is below 55%, which is why our bluff loses the expected profit.

8. Limitations

Let's turn to the elephant in the room. The truth is that MDF performs poorly in a vacuum. MDF makes one MAJOR assumption that limits its utility as a separate metric.

MDF suggests that bluff does not have equity.

In most cases, this does not reflect reality. In real poker, bluff usually have some equity to the river. For example, you can semi-bluff with draw – even simple hands with higher cards beat some part of your opponent's valley range.

So how does that make a difference?

9. When the return check has equity

When bluff has an equity in a return check, your goal changes — instead of just going to zero, you need to make the bet and the check equal in expectation. If, for example, an opponent bluff on the river with hands that have some showdown velle, apply MDF only to those hands that can beat his bluff. It makes no sense to apply MDF to hands that are not bluff-catchers, because they lose with a check in any case.

Example

Villain makes a Push on the river in position, and his bluff has 20% equity when the check is returned. What percentage of hands should you protect so that his bluff is indifferent to the bet and the check?

Your task is to equalize the EV of the bluff and the EV of the checkback. Since the EV of the checkback is 20% of the pot, we substitute this value into the equation:

1. EV bluff = 0.2 × (pot) = (% fold × pot) – (% call × bet)
2. 0.2 = (1 – call%) – call%
3. Call% = 40%

If his bluff didn't have equity (0%), you'd have to defend 50% MDF. However, since bluff retains 20% equity, you can fold more often and defend only 40%.

• Our goal is to make his bluff EV = EV check

• Equity check: check EV = 20% pot

• Hence: EV bluff = 20% of the pot (if we are not defending enough when the villain is bluff with a showdown valley)

10. When bluff preserves equity against calls

Villain makes a pot-beta Push on the turn, bluffing exclusively with draw that retains 20% equity against your call range. Since the EV of the check with these draw is also 20% of the pot, you need to determine how widely to defend to make the opponent's bluff indifferent between the bet and the check.

• Your goal is to equalize EV bluff and EV checkback on the turn: 

EV (bluff) = EV (check) = 20% pot

Taking into account the equity draw at colle, the equation EV takes the form:
0.2 = (fold% × pot) + call% ((win% × (bet + pot)) – (lose% × bet))

Substituting values:
0.2 = (1 – call%) + call% (20% × 2 – 80%)

Solving the equation, we get:
call% = 57%

Thus, to balance the protection against these bluff, you should call 57% of your range. A more intuitive way to interpret this is that a bluff brings less risk (compared to a pure bluff) because it has equity at stake. Push the size of a pot with a draw of 20% leads to about the same ratio of risk and profit as Push in the amount of 75% of the pot with a pure bluff (0% equity). Pot bet Push with a little equity in this sense is almost the same as if the Push was smaller, but without equity at all. That's why you can often bet more on boards with more draw. However, in practice, we rarely try to make strong draw indifferent to bet and check.

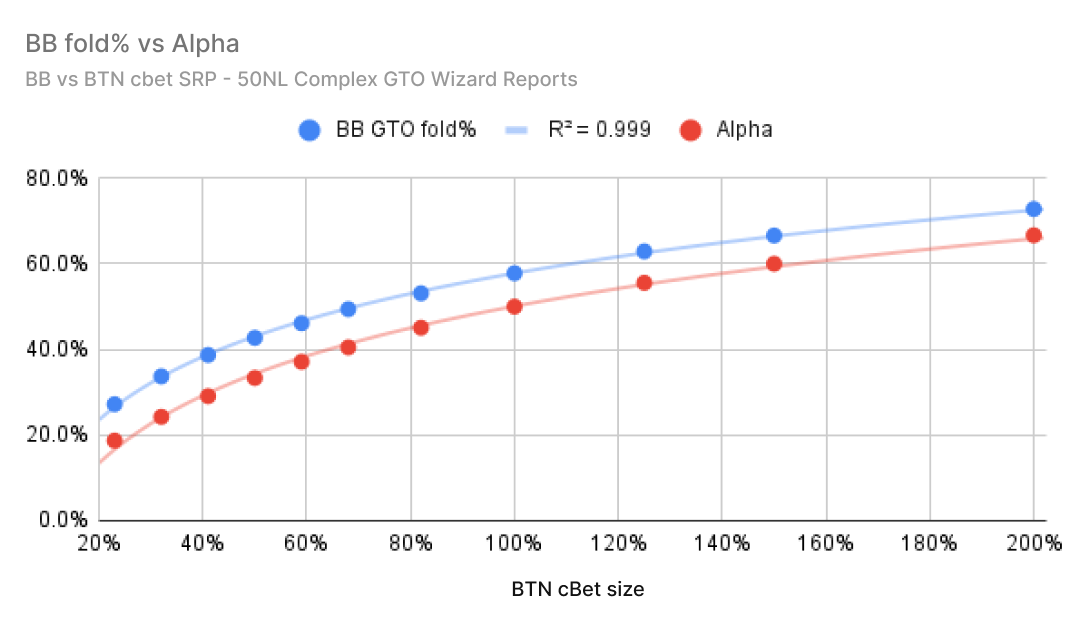
11. Is the TRP subordinate to the MDF

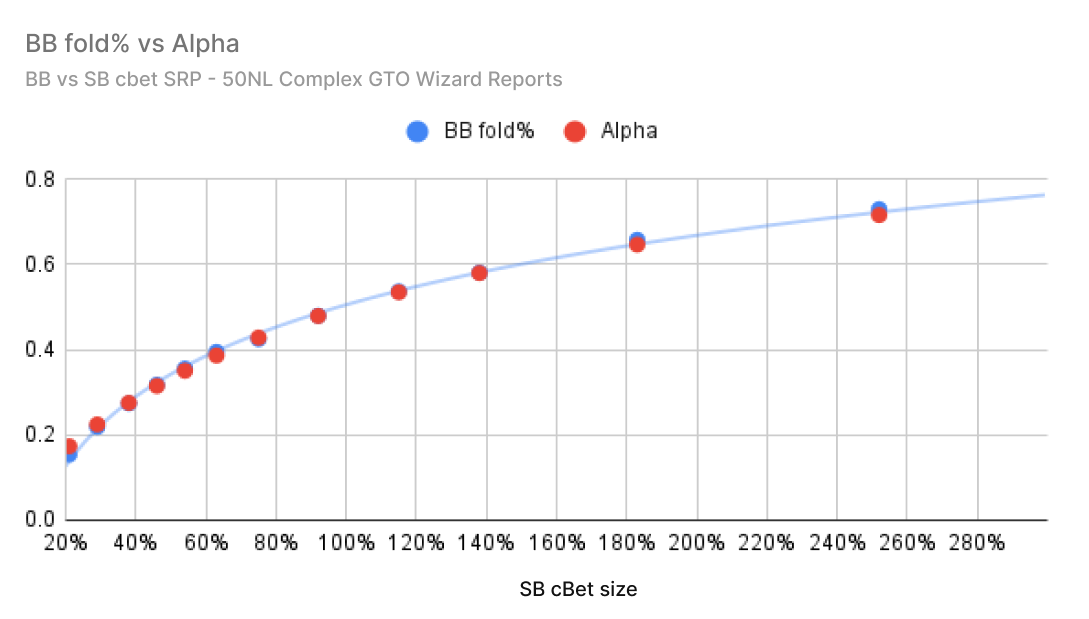
Using complex GTO Wizard reports, I plotted the GTO fold frequency (blue) versus the estimated MDF fold frequency (red). These reports cover all 1755 strategically different flops. On average, BB vs. button is constantly overfolding at any bet size on the flop.

BB vs. Button button graph

Here is the same report made for SB vs BB in SRP (single raise pot). In this case, the defender has a position and therefore on average collides much closer to the MDF.

SB vs BB Chart

12. Insufficient protection

In theory, insufficient protection compared to MDF is quite common and in many situations proves to be the preferred strategy.

The main disadvantage of a call strictly according to MDF is that it deprives the opponent of the motivation to bluff with hands that have non-zero equity in the return check. This is not a problem when it comes to nuts or completely airy bluffs, but in a real game, most bluff retain some equity. As a result, in most cases, insufficient protection turns out to be less risky than excessive protection.

Generally speaking, you should protect less than an MDF when:

1. You are out of position on the flop or turn (IP bluff have EV when check is returned).
2. When the villain is bluff with his hands ready (apply MDF only to the hands that hit the bluff).
3. When the enemy's check-backs have EV.
4. In an exploit, against opponents who play most often only with a velly value.

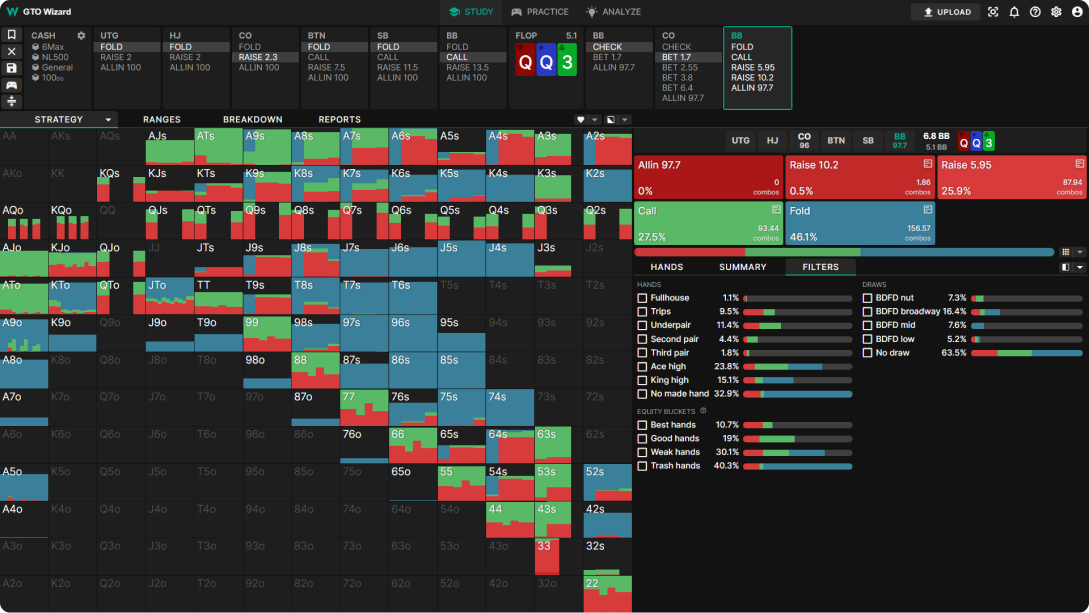
Here's an example:

CO rises, BB calls. Flop QQ3r (“rainbow”) 
Most CO bluff on this board have significant equity. Moreover, BB simply cannot realize its equity. As a result, the BB player on this flop will have to significantly overfold. CO counter-betite 33% of the pot. The MDF theory states that BB protects about 75% of its range and folds no more than 25% against this size of the c-bet. However, the solver resets almost half of its range!

Remove

 

Add item

13. Excessive protection

Excessive protection compared to MDF is quite rare, but in theory it does occur. As a rule, we see excessive protection in situations where the aggressor's bluff retains equity against the call range. In terms of operation, you can overprotect yourself when your villain bluffs a lot bluff.

Generally speaking, you should protect yourself more often when:

1. Villain pushes from early positions on boards with a lot of draw.
2. In a position where the villain is bluff with the draw retaining the equity.
3. On boards where splitting is very likely.
4. An exploit against actively bluffing opponents.

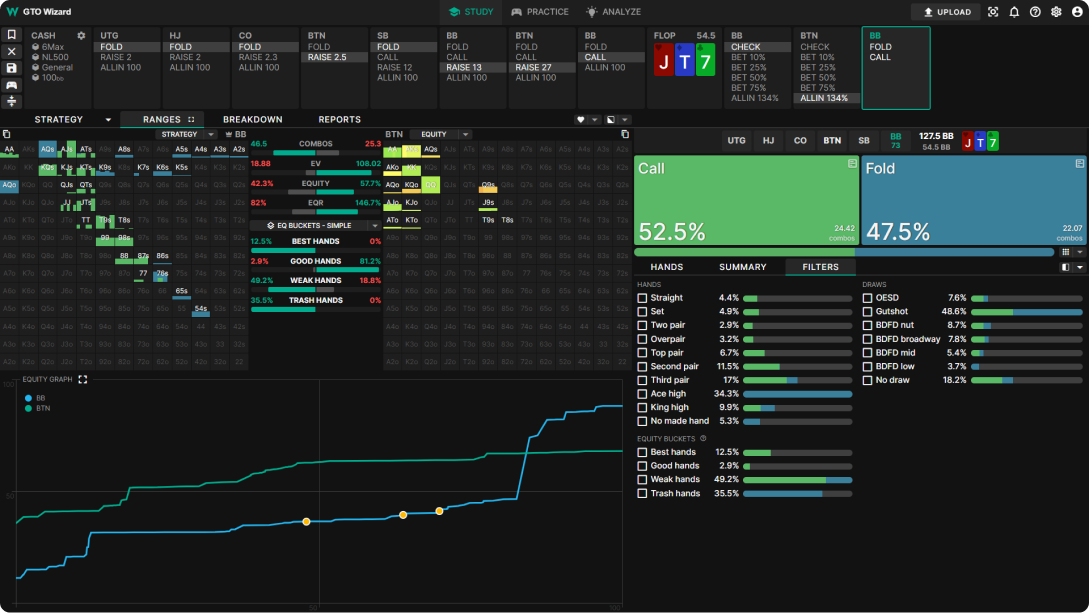
For example, here's an interesting spot.

This is a BTN game against BB, 4 bet pot, where BTN puts 134% on the flop. According to the MDF, BB has to fold 134/234 = 57% of its range and call approximately 43% of its range. However, solver believes that you need to call as much as 10% more often!

Remove

 

Add item

14. Conclusion

The minimum protection frequency is a shield used to prevent your opponent from confusing you with a bluff villain.

An alpha is a sword used to determine how often you need an opponent to villain to fold to justify the risk of bluff at a certain amount of your bet.

This metric is not perfect because it assumes that a bluff has no equity. However, this is a useful guide to roughly determine how widely you need to defend, or roughly how often you need to see a fold. You should make operational adjustments if you think your villain is bluffing too much or not enough bluff. Do not rely on MDF as a support in all situations, use it only as an average in a vacuum.

GTO strategies quite accurately repeat MDF in the position and strongly refold out of the position (on average). This concept obviously has value and can be applied much more than we have shown in this article. For example, you can use it to determine approximate thresholds for the values of different lines. We hope you now have a better understanding of the theoretical and applied applications of Alpha and Minimum Protection Frequency.