Translated with the help of AI. We apologize for any errors and would appreciate your help in correcting them.
Translated by order of the educational portal university.poker
Original source: GTO Wizard
“Bank pot geometry” means such a bet from the bank share on each street that you go all-in to the river. This bet strategy is also called “geometric bet size” or “geometric bank growth” sized pot. Geometric bet has one important effect: this strategy maximizes the number of chips your villain puts into the pot. If you want to stack-off the entire effective stack to the river, then the geometric bet will force your opponent to use the widest theoretical protection. In this article, we will look at the theory of bank geometry, why it forces the opponent to defend himself more broadly, consider examples and discuss the limitations of this strategy.
1. Maximize your opponent's defense
Why does the geometric bet maximize the opponent's calls?
Let's say you have two goals:
- Place all the chips on the river.
- Force the opponent to make a call on as many hands as possible.
There are an infinite number of bet strategies that can achieve this. You can make huge bets, then small bet bets, then medium bets. Or overbet twice. Or check-check-push. But which bet strategy is most effective in order to make the opponent's call the widest?
Of course, the geometric size of the bet! Bet of the same share of the pot on each street theoretically maximizes how widely the villain makes the call in general and how much money is deposited in the pot on average. But why? We can estimate how extensively the villain is protected using the minimum protection frequency (MDF). Multiply the MDF on each street to find the final call range.
Example:
- Pot is $100;
- Stack is $1300;
- Let's start with the flop.
Consider two bet strategies:
- Strategy: Push $1,300
- Strategy: pot bet on every street

Strategy A | Strategy B |
Villain makes a call: 100/(100+1300) = 7% of his range. | Villain makes a call: 50% * 50% * 50% = 12.5% of their range. |
| Villain contributes: 7% of his $1,300 stack for a total of $91 | Villain contributes: 12.5% of his stack in $1300, which in total is $162.5. |
Strategy B assumes that the villain invests almost twice as much money in the pot, which does not even include the bet that he called on the earlier streets and folded before the opening. If we take this into account, the total contribution of the opponent approaches $237.
2. How many streets are left
- The pot is $6;
- Stack is $97.
The geometric size of the bet depends on how many streets (bet) are left.
Fewer streets require larger sizes to exhibit on the river: stack-off
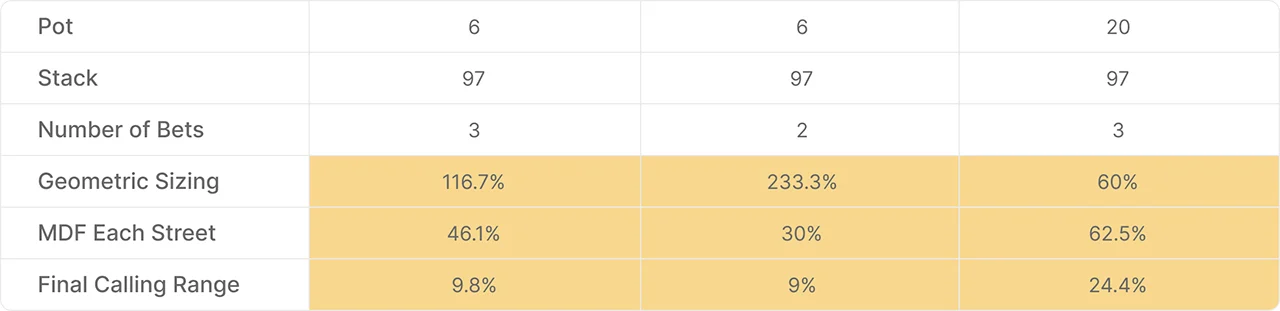
Pot, effective stack, number of bet, geometric size, minimum protection frequency on each street, total call range.
The general formula for finding the geometric size of the bet is as follows:
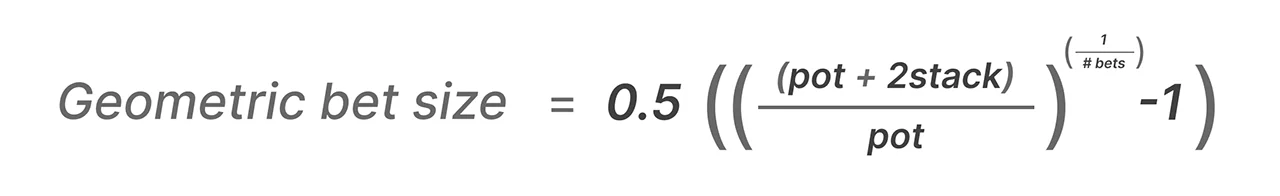
However, the calculation of this in the game is superfluous. It is better to simply estimate the geometric size, thinking about the size of the stack and pot on the river.
3. Smoothness of bet
Let's define the “smoothness” of your bet strategy as the standard deviation of all your bet sizes (in %) on each street. We have created a spreadsheet with 400 different betting models (all bet on the river). Next, we plotted the smoothness of bet rates depending on the total amount of investments. The chart below shows that the smoother the bet strategy, the more money goes to the pot. The vertical axis shows how much money the opponent invests in the pot. The horizontal axis shows the deviation (spread) between the sizes of our bet on the flop/turn/river.
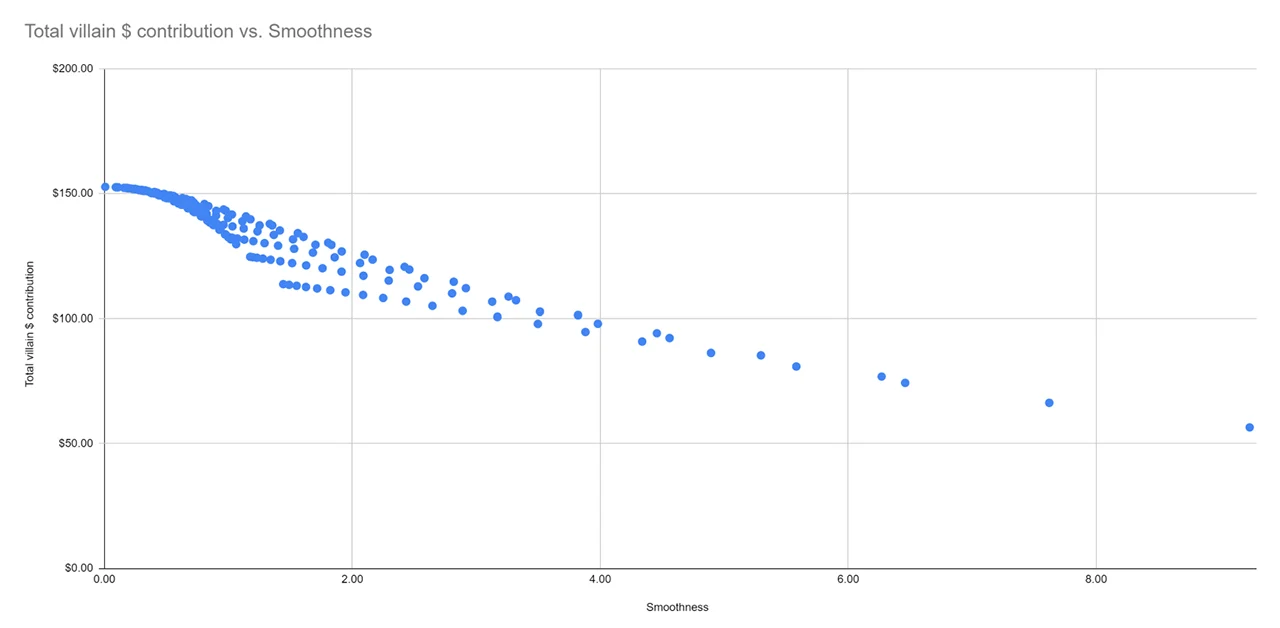
The range of the opponent's call expands in proportion to the smoothness of our bet. The further our betting model deviates from the geometric one, the less often it needs to call us to deprive us of a profitable bluff. That's why you expose yourself more secretly when you play with deeper stacks. The benefits of nuts become more valuable as the exposure range narrows. Next, we will plot different betting strategies depending on how much money the villain invests in the pot. Please note that he contributes the most money to the bank when the size of our bet on the flop/turn/river is the same (as a percentage of the pot).
Bet on the flop, on the turn and the river, the total investment of money by the opponent:
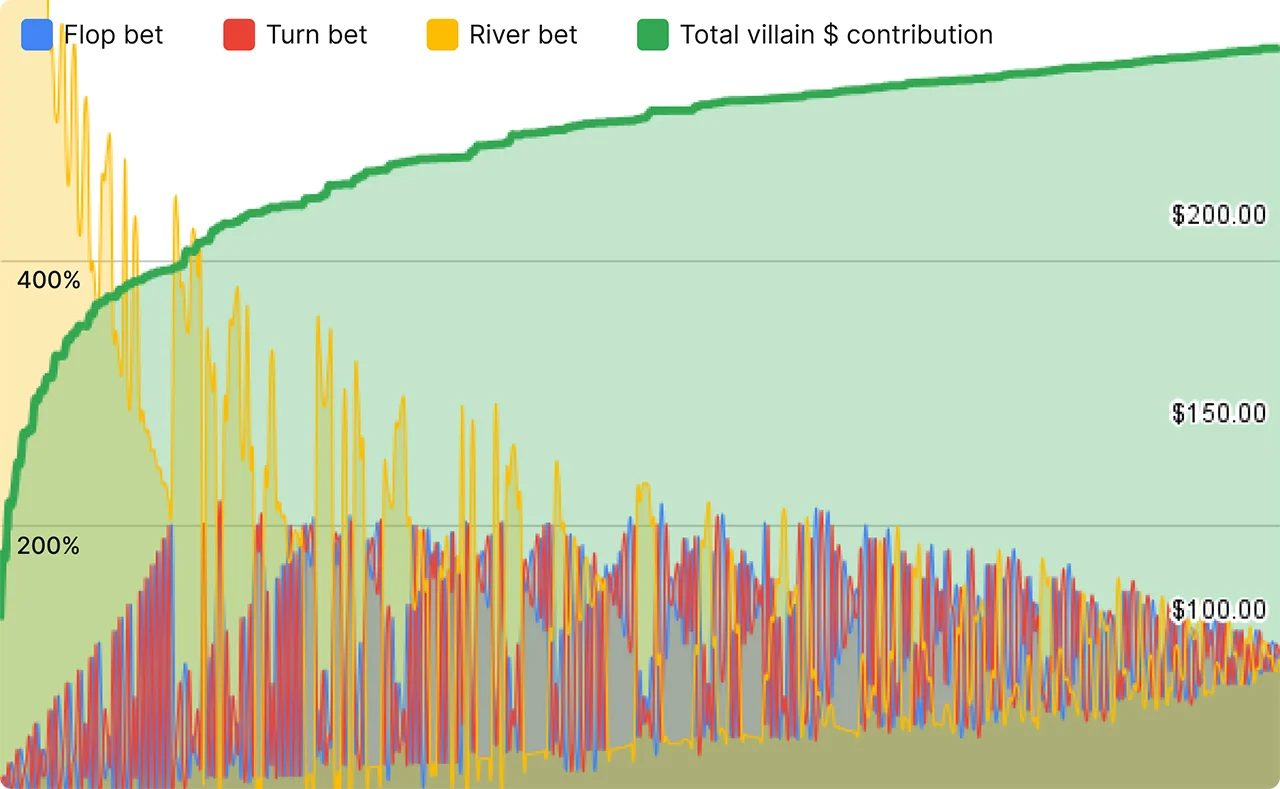
We've attached a link to the spreadsheet here so you can play with the data. You can try different sizes of stack and pot.
4. When to place a geometric bet in poker
GTO strategies usually use geometric sizes of bet when they want to maximize the value with a big nut advantage. This works better when your range is polarized and your opponent's range is trapped. The geometric bet strategy is derived from the MDF (minimum protection frequency). MDF works for the most part only in opposing the polar range against bluff-catchers. But, you should still make geometric bet when you have a big nuts edge.
- Example: one of the most common examples is trial-beta on the turn.
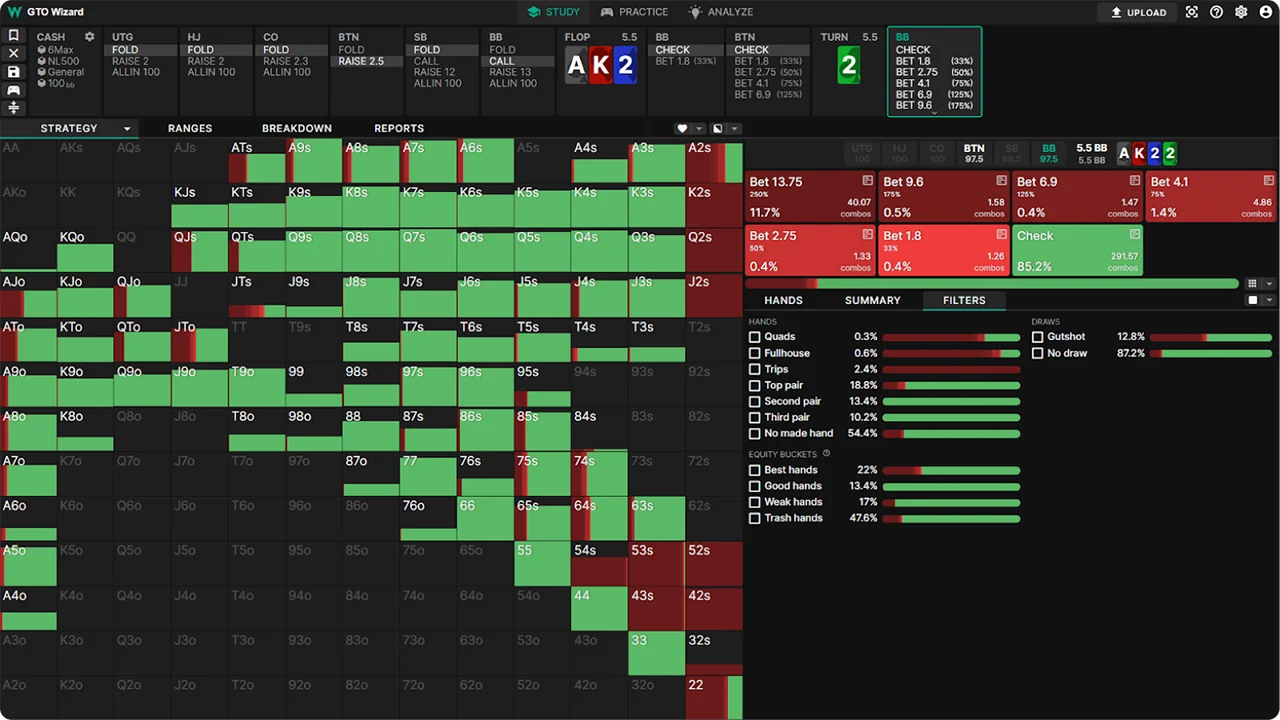
Example 1: Trial bet on BB against a player in position (single-raise pot)
Here we see the probe bet BB vs BTN strategy on the A-K-2-2 rainbow board after everyone has waited for the flop. There are 5,5BB in the pot, 97,5BB stacks and there are two streets left. The geometric size here is 252% of the pot. As you can see, GTO's strategy here is to place geometric bet or no bets at all.
BB has the edge of nuts in thrips, so he uses this edge as much as possible to stack-off to the river.
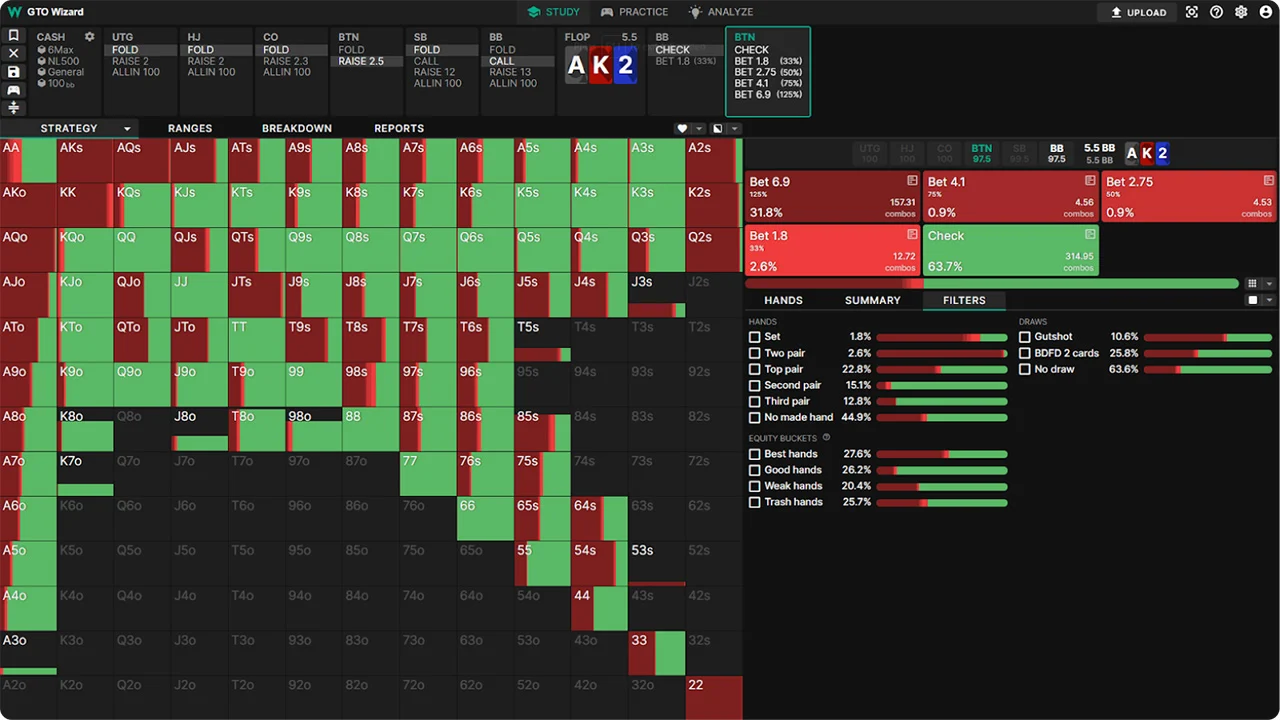
Example 2: c-bet at position vs BB
We see a similar strategy on the flop in position.
Here, BTN has a big edge in the form of top pairs, and it presses with them using the geometric size of the bet on three streets:
5. Non-geometric strategies
Let's look at our goals and assumptions:
Objectives | Assumptions |
| Invest all the money to the river. | Our opponent will defend according to MDF. |
| Force the opponent to make a call with as many hands as possible. | Our nutritional hands will remain nutritional to the river (this is a hidden assumption). |
These goals and assumptions are not necessarily true. A geometric bet strategy is designed for perfectly polarized situations, but in practice this rarely happens. A perfectly polarized range consists only of invulnerable nuts and pure bluff (relative to the range of the opponent). Equity is so static that no hand can improve or deteriorate. But real poker is full of draw, and equity is not static. Most hands may improve or deteriorate towards the river.
More importantly, you rarely have enough nut hands to implement this strategy. Most middle hands can't play the stack without overplaying their value.
GTO strategies are not geometric in most situations. GTO rarely uses a geometric strategy to the tern, as the range is too close and the equity is too dynamic. Equity is largely fixed on the later streets and the range becomes more polar, stimulating the geometric dimensions of the bet. When the equity of opponents is close to each other and can be changed more easily in the early streets, geometric sizing is not about this case.
6. Conclusion
Geometric bet is designed to put all the money to the river, while maximizing how widely the opponent needs to defend. This bet scheme is derived from MDF (Minimum Protection Frequency) and is ideal for polarized scenarios solely against bluff catchers. However, it does not always fit the situation in the real world, since the range is rarely perfectly polarized. The geometric size of the bet is most useful when you are pressing with a clear advantage in nats on static textures (your nats hands are most likely to remain nats to the river). This strategy becomes more common in GTOs on later streets when the range is delineated in more detail.




