Translated with the help of AI. We apologize for any errors and would appreciate your help in correcting them.
Translated by order of the educational portal university.poker
Original source: GTO Wizard

When multiple bet sizes are used, frequent mixing of these sizes is often implied, thereby blurring the heuristics underlying size decisions.
If any hand can place bet of any size, then what's the point of using multiple sizes? How would you ever choose in a real game situation what to use with this hand?
This is where solvers come in handy, but not to memorize the output, but to learn from it. Your goal when working with solvers should be to understand why solutions look the way they do. Understanding the underlying driving forces will allow you to apply them in many situations, not just the one you are currently studying. The node lock feature offers a powerful new tool to explore complex solutions.
It allows us to check the function of each strategic option (bet, check, raise, etc.) in the strategy, eliminating this option or recording the opponent's response to see how our incentives change. In this article, we'll take a closer look at a common solution on the flop (betting less or more) to demonstrate how blocking nodes can help your research.
1. Finding clean strategies

You can build your intuition around what motivates you to use a certain bet size (or other strategic option). The same logic applies to check, call, raise, and even fold), looking for hands that simply perform this action. These are hands that are not indifferent when you have a clear incentive to prefer one option over another. In the absence of any clean strategies, look for the hands that perform this action with the highest frequency.
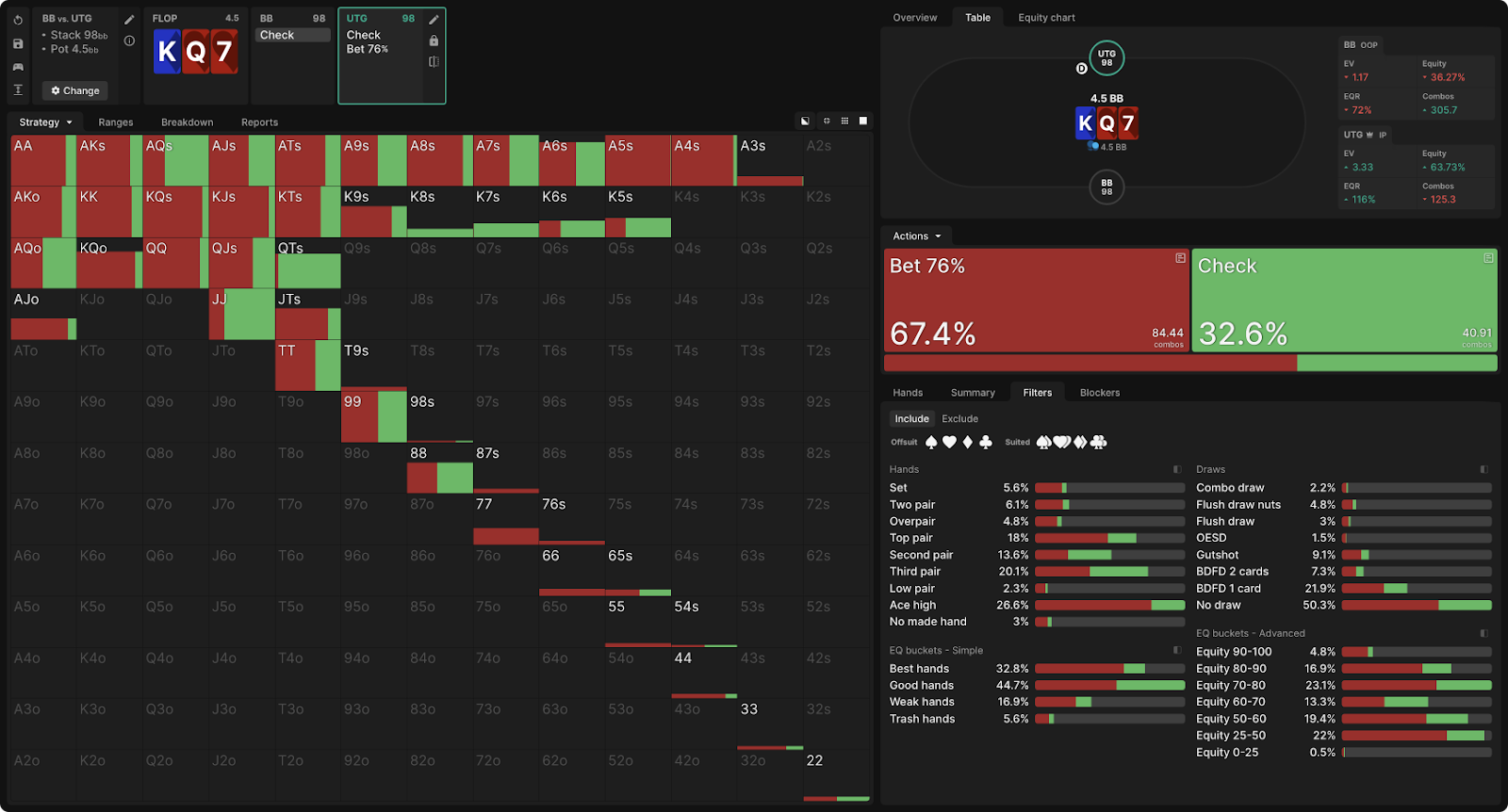
- Let's look at an example from a cash game with 9 players and 100bb stacks. UTG makes an open-raise 2bb preflop, BB calls, and they see the flop:
After the check BB UTG can make a check or a bet of 76% or 24% of the pot.
As you can see, the solver never checks (this 1% is an error — if the simulation were run to 0 exploitability, it would disappear), but it largely uses both bet sizes and most hands mix between them:
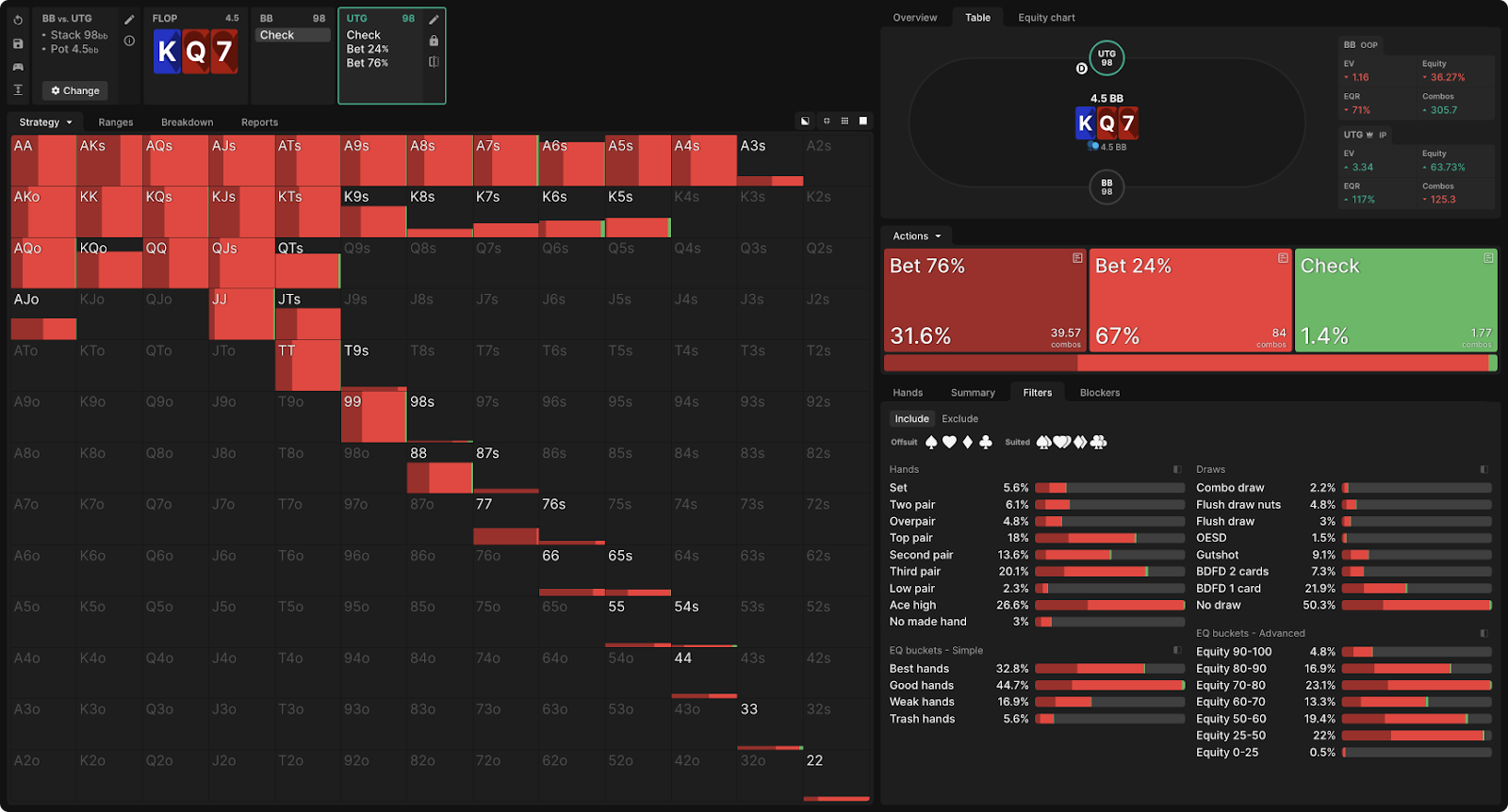
If you want a simplified strategy on the flop — not a bad idea, if you are new to GTO — then you can infer from this result that a small sized bet with your entire range would be an acceptable strategy. But these big bet's are there for a reason. Determining this reason will lead you to increase your EV compared to a simplified strategy. Start by looking for exceptions, hands that place bet purely one size or the other. AQs, K8s, K7s and K6s are immediately striking. If you dig deeper, you will see that some other mixes depend on the suit.
Example: with rare pocket pair with a worm, as a rule, mix, but without a worm, make bet only of small size.
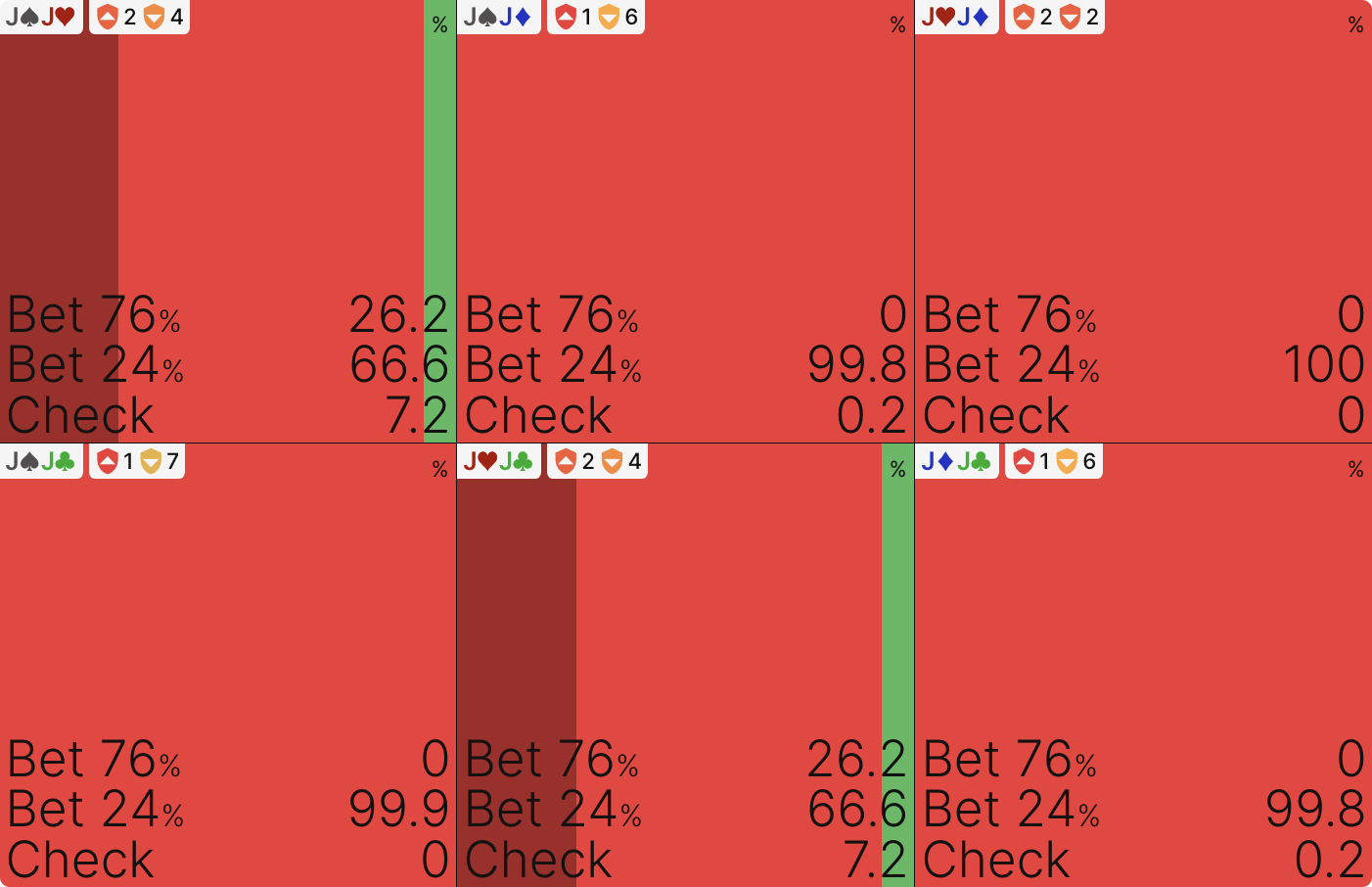
Example: some traces of this behavior can be found for hands such as K5s.

What do these hands have in common? They all have middle strength, fairly strong hands, ahead of most of the BB range, but do not feel well against the top pair or better. This explains the reason they prefer a smaller size: they benefit from denying equity and getting a call from weaker BB hands (those that can fold on a bigger bet). However, if they put too much money into the pot, they will concentrate the BB range around the strongest hands they play poorly against. Thus, they avoid a larger bet size and bet exclusively 24% of the pot.
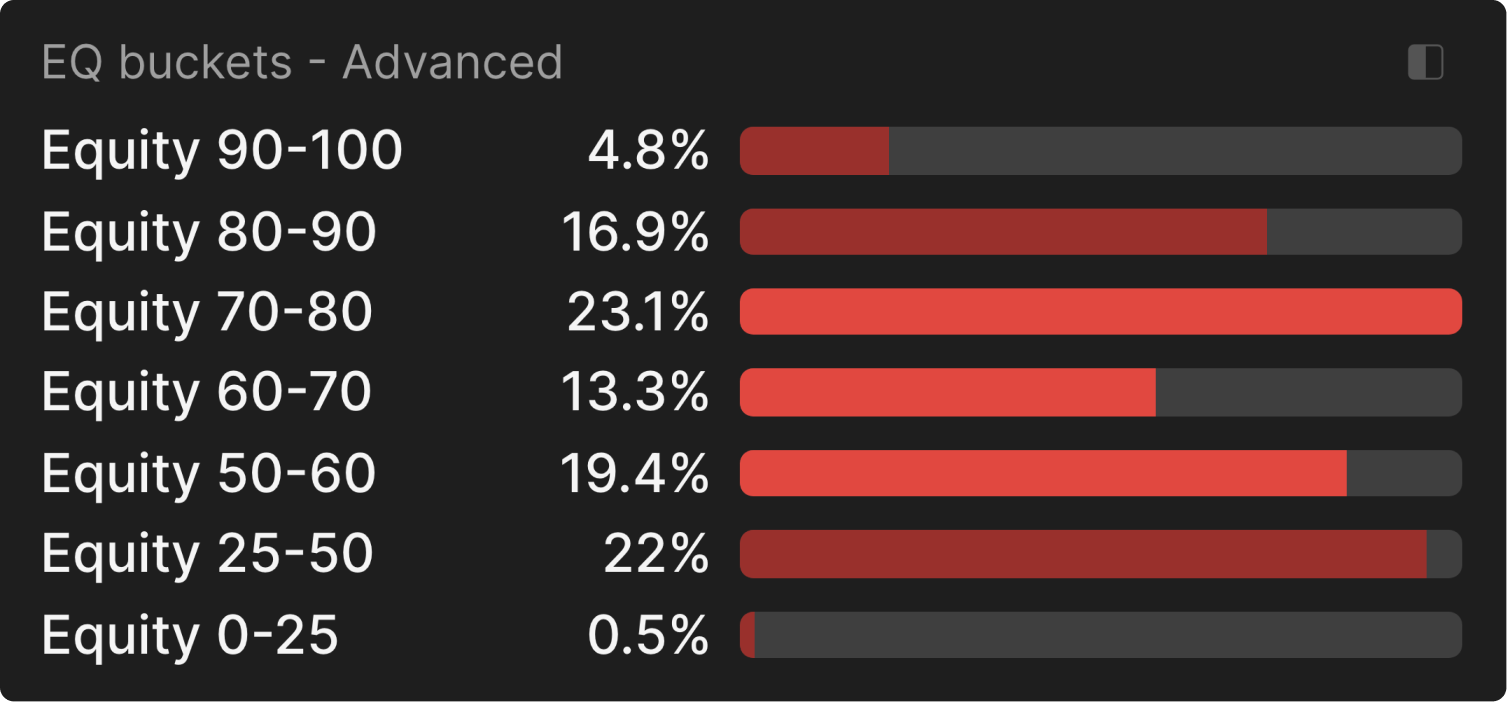
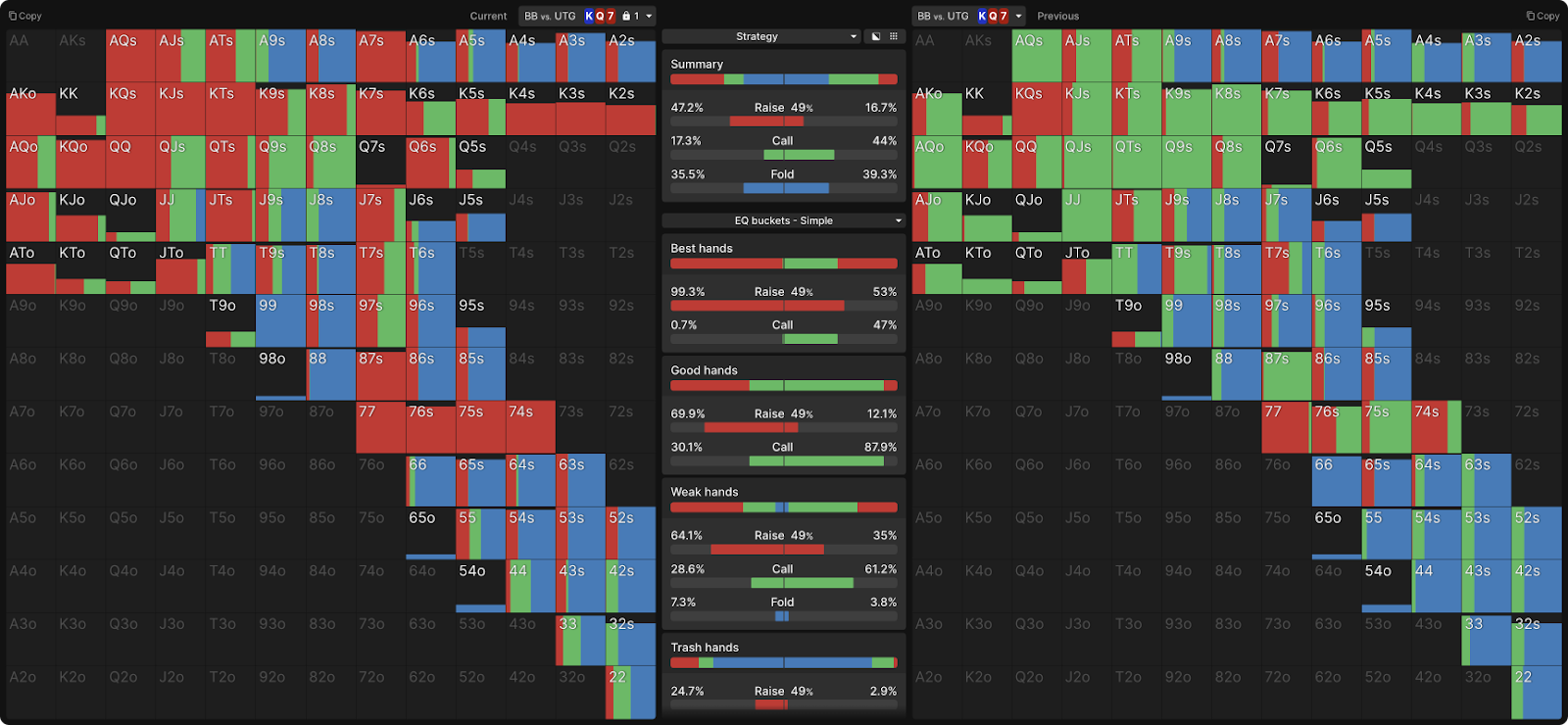
We can confirm this by looking at the equity folders, where we see that UTG most often uses a big size with the strongest and weakest hands, and a small size mainly with medium hands:
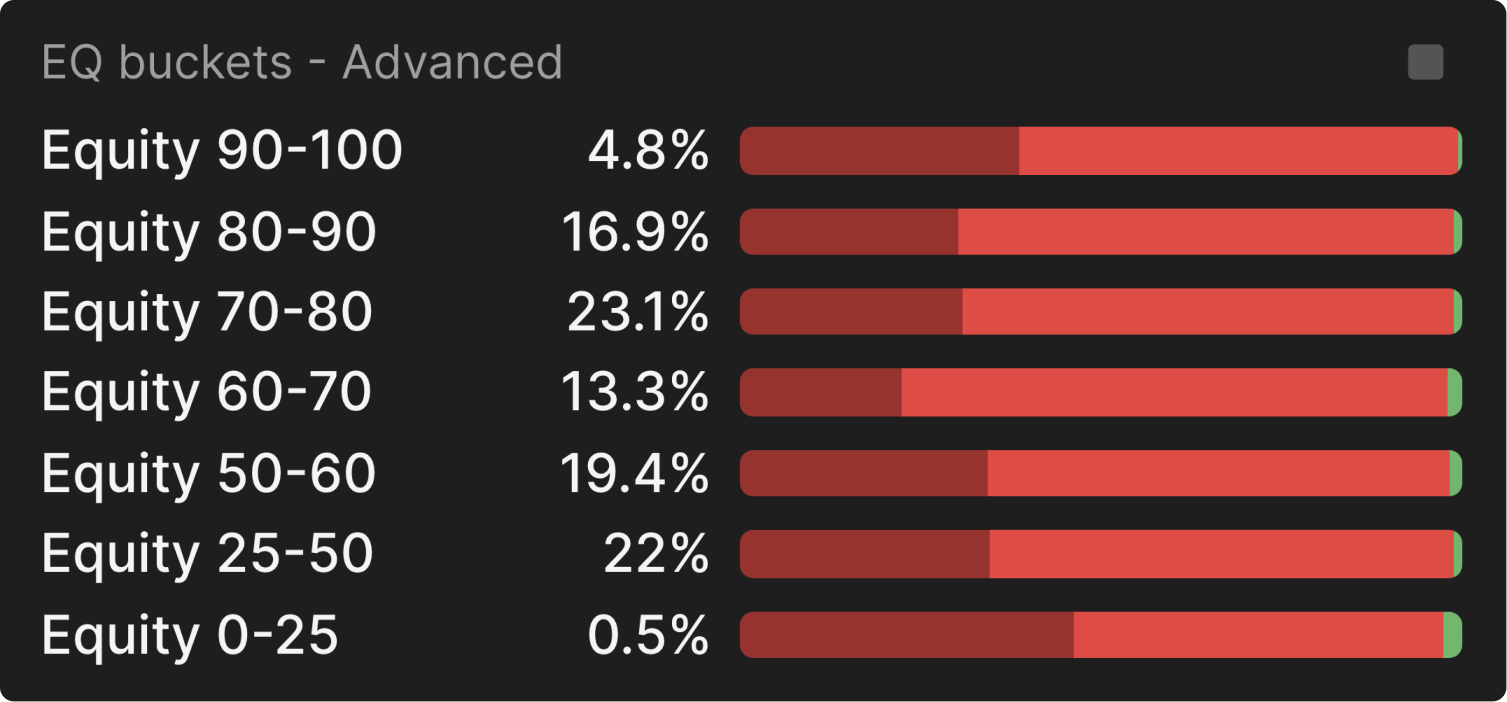
The more you bet, the more you concentrate your opponent's range around their strongest hands.
This explains why a small bet size is used. UTG wants to place bet with their average hands, but a big size of these bet will not be profitable . We can prove this with a special solution, where we block the UTG strategy so that it will place bet only in the amount of 76% of the pot. In this scenario, UTG cannot profitably place bet with its entire range.
It is these hands of medium strength that make up the range of the check:
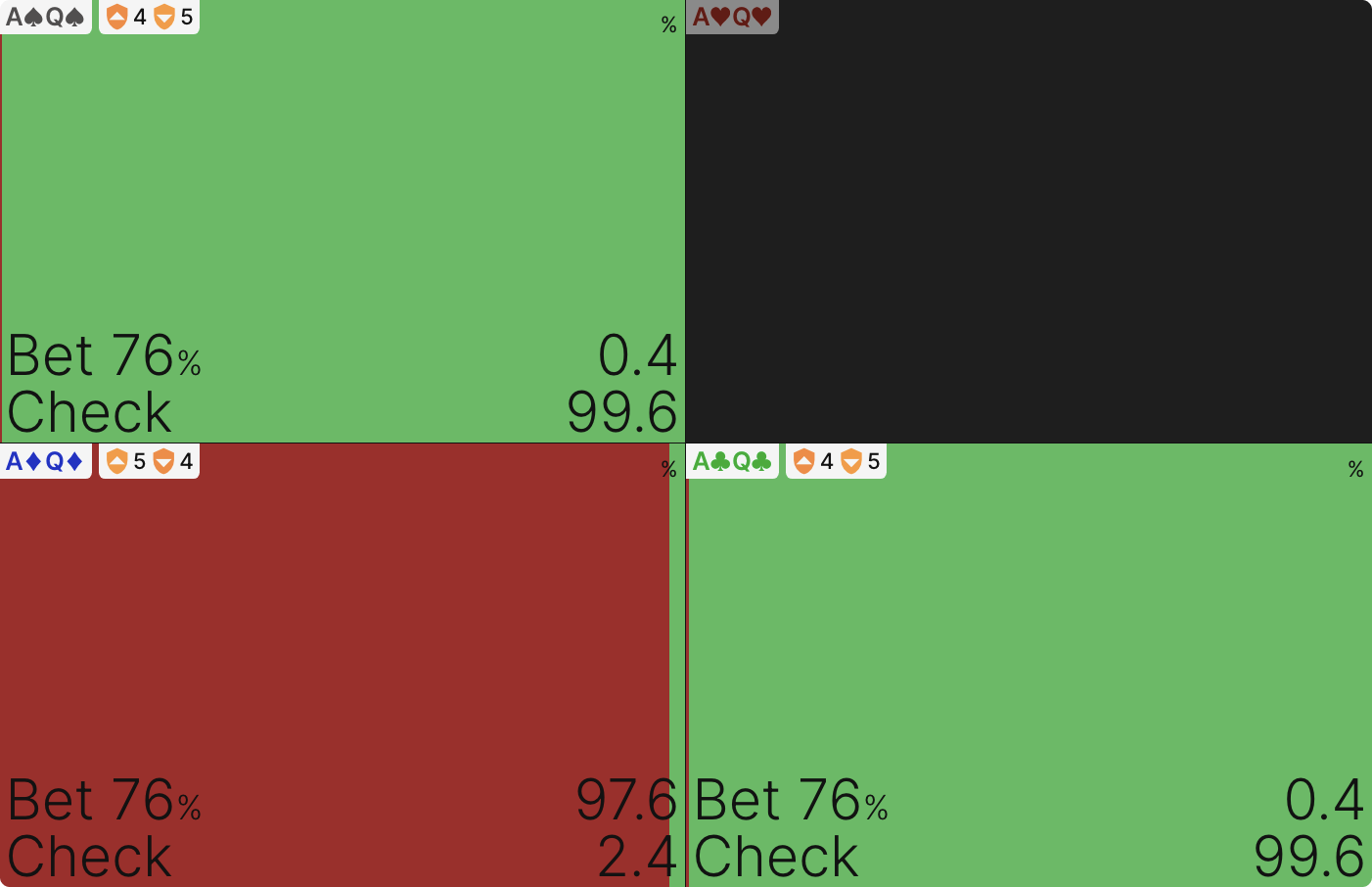
2. Explain the anomalies
The main goal of the small extended bet seems to be to leave a lot of medium strength hands in the UTG range. However, this is not a complete explanation as it does not take into account the presence of strong hands such as AA and K7s in the small bet range. Why do these hands not prefer a strictly large bet, given that they benefit a lot from the growth of the pot against the top of the BB range? A common explanation is that these “monster hands” “protect” the middle hands by keeping BB from raising, but this is a bit misleading. This implies that the strongest hands are sacrificed, giving up the higher EV option for the sake of other hands in the UTG range. This kind of sacrifice is never a feature of GTO solutions. Solvers do not abandon the EV of one hand to increase the EV of the other.
If a hand is mixed between several bet sizes, then in equilibrium it has the same EV with all of them. Solvers never sacrifice the EV of one hand to increase the EV of the other.
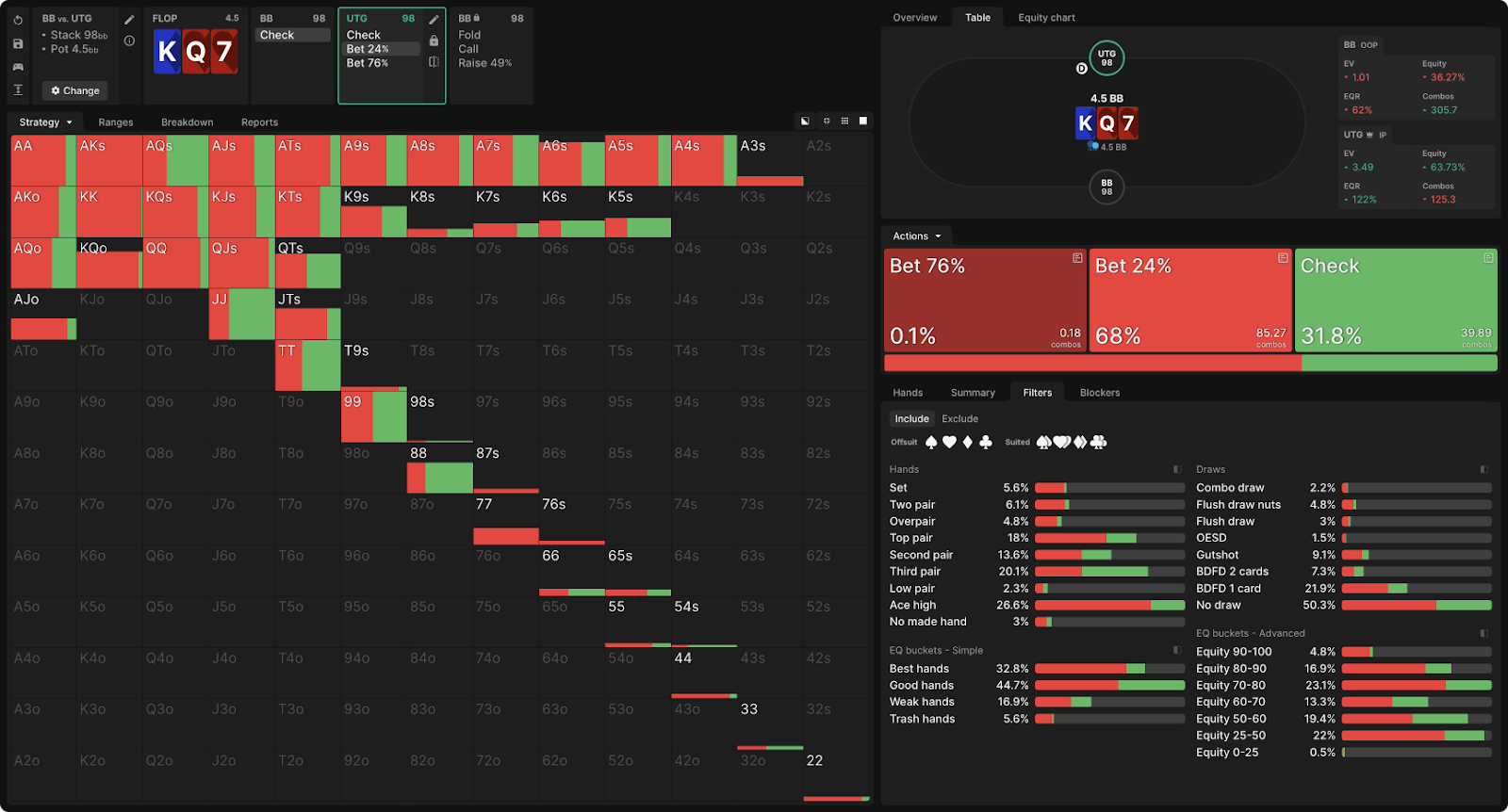
This raises a new question: where does the EV in the small bet line for stronger hands such as AA and K7s come from? How does a small bet win as much as a big bet? A good way to approach such questions is to explore from the opposite. What would happen if UTG never made small bet with the strongest hands?
We can test this with a custom solution in which we force UTG to place big bet with the strongest and weakest hands and small bet with medium hands:
Fixing such a strategy, we will see that BB drops on a small bet from this range about as often as on a small bet in a conventional simulation. The main difference is that BB increases three times more often!
You can intuitively understand how balance works by thinking in terms of balancing weights. For UTG, the EV of small bets with strong hands depends on the bet check rate BB. And for BB EV, the check-raise depends on the frequency of small UTG bet with his strong hands.
BB's

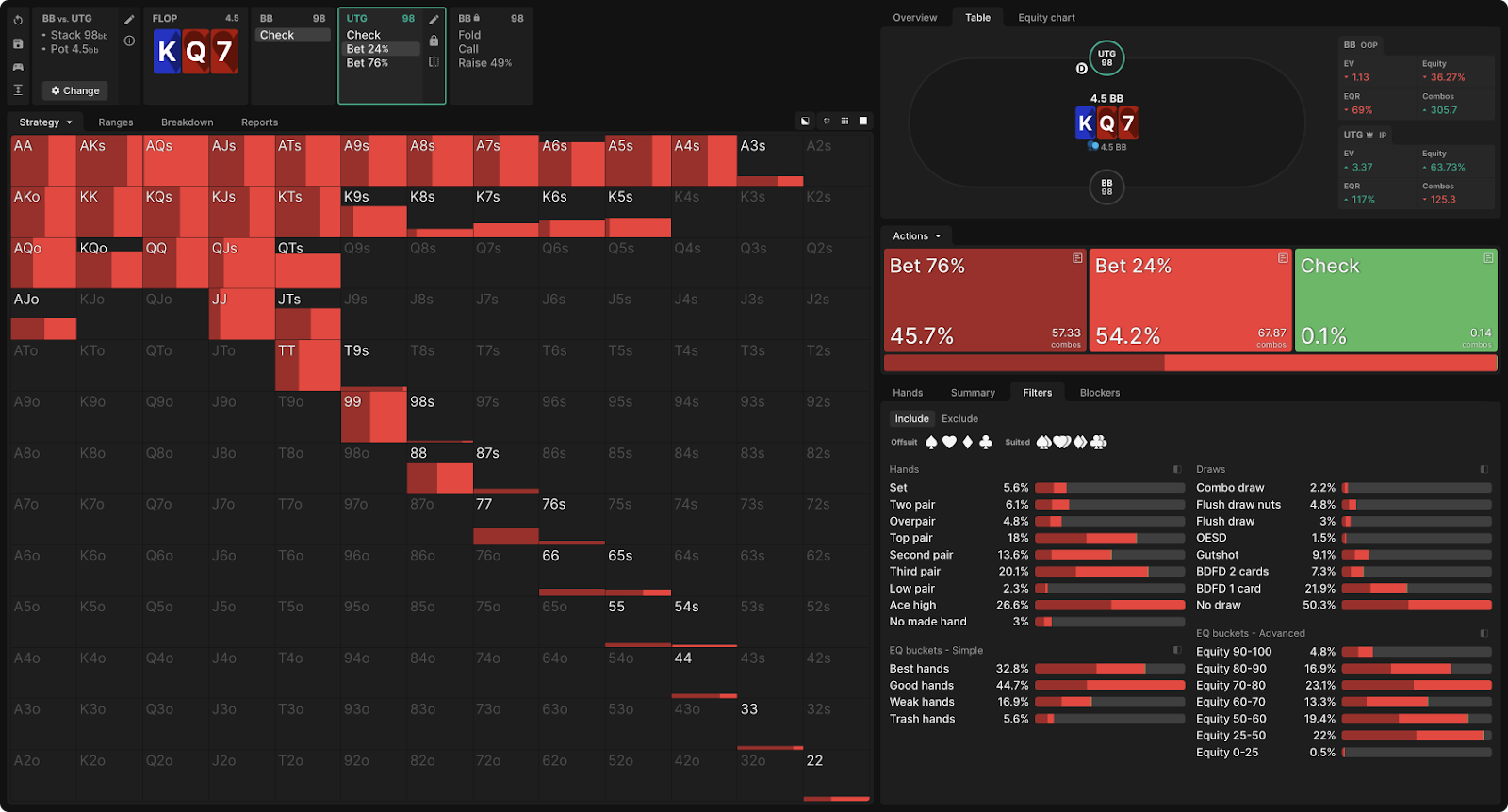
incentive to raising small bet comes from UTG's middle hands. His incentive to make a call comes from UTG's strong hands. When UTG chooses the right ratio of strong and middle hands in its small bet range, BB will be indifferent between raise and call with hands like ATo and 76s. Similarly, when BB chooses its raises frequencies correctly, UTG will become indifferent to making a big and small bet with its strongest hands. Strong hands don't sacrifice anything. They place small bet for their own sake because they expect to make exactly as much profit from that bet as they do from the larger bet. We will see this effect if we block the BB strategy so that it makes a check-raise twice as often against a small bet than in equilibrium.
Then UTG will completely stop using big sizing, because even his best hands now bring more money from small bet:
UTG also prefers to make a check with many of its weaker arms against such a hyper-aggressive racer, which gives rise to a new set of incentives. If the check range is weak, BB has a lot of incentive to attack it with big turn bets.
Indeed, when only one bet size is allowed, the solver chooses overbet almost 3 times the pot
with 21% hands on the turn :

If he chooses this overbet frequency correctly, then UTG will also have some incentive to check their strongest hands to provoke these overbets. Just as with the balancing between small UTG trap bets and BB raises, a new equilibrium is emerging between UTG check traps and BB overbets.
3. Make operational judicious calls
What does all this mean for you from a practical point of view? How does this help answer our original question about how to choose a bet size? Once you understand what your opponent's actions are encouraging you to choose each line, you will be able to consider which imbalances are more likely in this situation. With some hands, you have a preferred option, not much dependent on your opponent's reaction. If you can recognize these hands, you can play them accordingly.
When you think your hand is mixing variants because it is indifferent in equilibrium, then the EV of both variants will be close against a well-balanced opponent. So it doesn't matter which one you choose. This frees you from actions based on intuition, since even if you make a mistake and play a pure strategy to exploit a mistake that your opponent does not make, you will not lose chips (unless it is strongly imbalanced in the opposite direction from what you expected).
Once you understand which of your opponent's actions encourage you to choose each line, you can decide which imbalances are most likely.
Against an overly aggressive opponent, you would simply place small bet with your strong hands to provoke raises, as we saw in our example above. Against an overly passive opponent, you would just place big bet with the same hands, because he would not twist you often so that you could make money on it. Your opponent's imbalances should not be as dramatic as in our examples. We deliberately considered extreme manifestations to make the thought clearer.
Here is the strategy of continued UTG bet, if we fix the BB strategy so that it will make a check-raise half as often against both bet sizes (and never make a donk bet, which would otherwise make the solver to compensate for the reduced check-raise, but which a passive villain would not):
Strong hands still mix between both sizes, but in general a big bet size is preferable much more often. However, the same hands retain their preference for a small bet, such as JJ, K6, and AQ without the hearts.
4. Conclusion
Pure strategies indicate hands that have strong incentives to choose a particular line. Understanding these incentives also helps you understand why this line is strategically important. However, traps are also important, so it is rarely possible to choose a line only with “obvious” hands. Your opponent can understand what you are trying to achieve and tweak your game to thwart your plan. Blocking the strategy allows us to mimic this process.
We can block our strategy so that we play a less confusing strategy and see how the opponent responds to us. These responses motivate our own blended strategies, creating a balance between potential enemy exploits and our “traps.” Having dealt with all these heuristics, we can come to practical considerations to choose certain solutions in the game.
- So, we determined that medium strength hands strongly prefer small bets, while stronger bet hands choose between bigger bets to win more from calls, or smaller ones to win more from raises.
Both sizes are equally profitable in equilibrium, but your opponents won't play perfectly balanced strategies. Based on the heuristics you have studied, you can make decisions about which size will be better in a particular situation.